3165. Bicoloring
In 1976 the
“Four Color Map Theorem” was proven with the assistance of a computer. This
theorem states that every map can be colored using only four colors, in such a
way that no region is colored using the same color as a neighbor region.
Here you
are asked to solve a simpler similar problem. You have to decide whether a
given arbitrary connected graph can be bicolored. That is, if one can assign
colors (from a palette of two) to the nodes in such a way that no two adjacent
nodes have the same color. To simplify the problem you can assume:
·
no node will have an edge to itself.
·
the graph is nondirected. That is, if a node a is said to be connected to a node b, then you must assume that b is connected to a.
·
the graph will be connected. That is, there will be at
least one path from any node to any other node.
Input. Consists of several test cases.
Each test case starts with a line containing the number n (0 ≤ n ≤
1000) of different nodes. The second line contains the number of edges l (1 ≤ l ≤ 250000). After this l
lines will follow, each containing two numbers that specify an edge between the
two nodes that they represent. A node in the graph will be labeled using a
number a (1 ≤ a ≤ n). The last test contains n
= 0 and is not to be processed.
Output. You have to decide whether the
input graph can be bicolored or not, and print it as shown below.
|
Sample input |
Sample output |
|
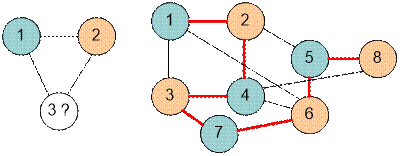
3 3 1 2 2 3 3 1 8 12 1 2 2 4 3 4 3 1 3 7 7 6 4 6 1 6 2 5 5 6 4 8 5 8 0 |
NOT BICOLOURABLE. BICOLOURABLE. |
SOLUTION
depth first search
Algorithm analysis
To solve
the problem, let’s use depth-first search. Initially, the vertices are not visited,
mark them all with color 0. As we go through the vertices, paint them in two
colors: 1 and 2. If the current vertex has color i (i = 1, 2), then the
next vertex, that we get at depth-first search, paint with color 3 – i. At the same time, check that two
adjacent vertices are not painted with the same color.
Example
The graphs given
in the samples are as
follows:
Algorithm realization
Store the
adjacency matrix of the graph in array g
of size MAX = 1001 (the vertices are numbered from 1 to n ≤ 1000). The array used
contains information about the vertex color. The global variable Error is responsible for the correctness
of the coloring: as soon as there will be found two adjacent vertices, colored in
one color, the variable Error will
take the value 1.
#define MAX 1000
int g[MAX][MAX], used[MAX], Error;
The dfs
function performs a depth-first search. Two parameters are passed to it: the
current vertex v and its color color. If the case of impossibility of
the required coloring has already occurred (Error
= 1), then exit.
void dfs(int v,int color)
{
If the case of impossibility of the required coloring
has already occurred (Error = 1),
then exit.
if (Error) return;
Mark the vertex v
with color color.
used[v] = color;
Look for an
unvisited vertex i, that can be
reached by continuing the depth first search. In this case, if the neighboring
vertex i is already visited, check
the condition that vertices v and i are colored in different colors. If
these vertices are painted the same color, set Error = 1.
for(int i = 1; i <= n; i++)
if
(g[v][i])
if (!used[i])
dfs(i,3-color); else
if (used[v]
== used[i]) Error = 1;
}
The main part
of the program. Read the number of vertices n
and the number of edges l of the
graph. Set to zero the adjacency matrix and the array used.
while(scanf("%d %d",&n,&l),
n)
{
memset(g,0,sizeof(g));
memset(used,0,sizeof(used));
Read the
graph.
for(i = 0; i < l; i++)
{
scanf("%d %d",&a,&b);
g[a][b] = g[b][a]
= 1;
}
Set the
value of the variable Error to zero,
and start the depth first search from the vertex 1, panting it with color 1.
Error = 0; dfs(1,1);
Print the result depending
on the value of the variable Error.
if (Error) printf("NOT
BICOLOURABLE.\n");
else printf("BICOLOURABLE.\n");
}
Java
realization
import java.util.*;
public class Main
{
static int g[][], used[];
static int n, l, Error;
static void dfs(int v,int color)
{
if (Error == 1) return;
used[v] = color;
for(int i = 1; i <= n; i++)
if (g[v][i] == 1)
{
if (used[i] == 0) dfs(i,3-color);else
if (used[v] == used[i]) Error = 1;
}
}
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
while(true)
{
n = con.nextInt();
if (n == 0) break;
l = con.nextInt();
g = new int[n+1][n+1];
used = new int[n+1];
for(int i = 0; i < l; i++)
{
int a = con.nextInt();
int b = con.nextInt();
g[a][b] = g[b][a] = 1;
}
Error = 0;
dfs(1,1);
if (Error == 1) System.out.println("NOT
BICOLOURABLE.");
else System.out.println("BICOLOURABLE.");
}
con.close();
}
}